ＣＯＬＯＲ No.150掲載前回（
No.149掲載）は、L*a*b*表色系とL*u*v*表色系の図上にマンセルグリッドとマクアダムの偏差楕円を示しました。
今回は、L*a*b*表色系の基になったアダムス(Adams)のクロマティック・バリュー空間(Chromatic
Value)とグレイサー(Glasser)らのキューブ・ルート空間(Cube-Root)を紹介します。
アダムスのクロマティック・バリュー空間
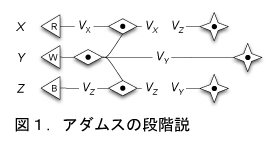
図1は1942年の論文で発表されたアダムスの段階説です。「三刺激値の非線形変換」と「 ヘリングの反対色説」で構成されます。
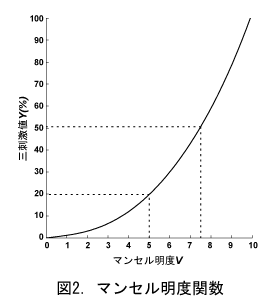
まず、非線形変換に図2のマンセル明度関数が使われます。明度Vから三刺激値Yを求めるのが本来の姿ですが、アダムスは順応後の三刺激値（XC, YC, ZC）を求め、この全てに適用して（VX, VY, VZ）を求めました。
続いて、ヘリングの反対色説に基づいて3次元空間の構成です。明度VYと反対色の（VX−VY）と（VZ−VY）を求めて、アダムスのクロマティック・バリュー空間とします。
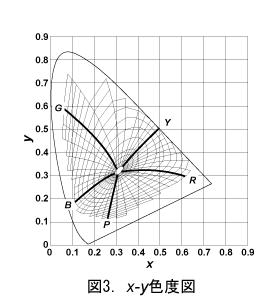
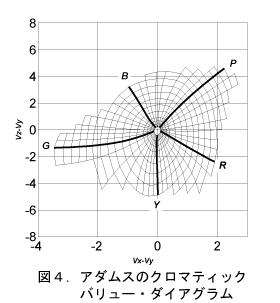
図4にマンセルグリッドの明度5を示します。前回のx-y色度図（図3）に比べ、マンセルグリッドの等色相線の方位性、等彩度線の歪みと等間隔性が改善されています。ただし、横軸と縦軸の目盛から比率を改善する必要が分かります。
グレイサーらのキューブ・ルート空間
1958年、グレイサーらはマンセル明度関数の代わりにキューブ・ルート関数を使った論文を発表しました。
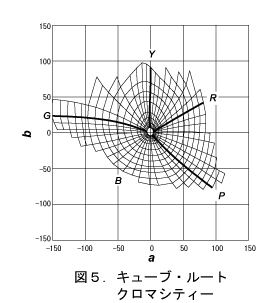
明度Lと反対色のaとbによる空間です。 図5にマンセルグリッドの明度5を示します。横軸と縦軸の目盛の比率が改善されています。
L*a*b*表色系までの変遷を表1に示します。
いずれも「三刺激値の非線形変換」と「ヘリングの反対色説」が基本であり、非線形変換に使用する関数と空間展開に使用する係数が少々異なるのみです。次回は、その係数の違いについて、数式の比較を行います。（那須野信行）
 |
 |
 |
 |
 |
|
 |
