<研究2部報>CIEDE2000色差式について(その4―青色領域の傾き補正)
 COLOR No.174掲載
COLOR No.174掲載
前回は、無彩色付近での歪み補正におけるスイッチング関数Gの役割について解説した。今回は、「青色領域の歪み補正」について、以下に示す対象の式を使い解説を行う。
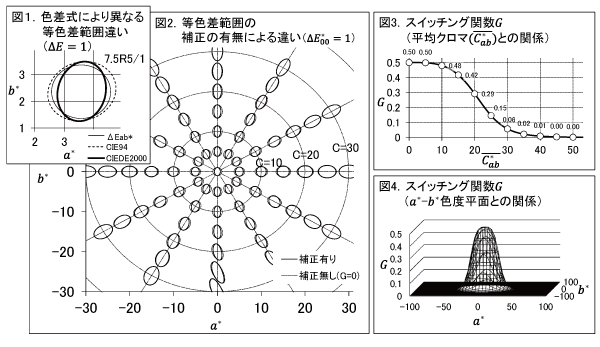
「青色領域の歪み補正」について、CIEDE2000色差式 ∆E00(式1)で計算した等色差範囲()の結果が(図1)であり、(式2)の回転関数RTによる補正有りは実線の楕円で、補正無しは点線の楕円で示されている。その際に使用した基準色は、色相角差∆hab=5°、彩度差
の間隔で設定を行った。楕円の重なりを比較すると、補正がない場合の点線の楕円は無彩色軸を中心に等しく外周部方向に伸びて広がっているが、回転関数RTによる実線の楕円では色相角habが230°~320°の範囲で回転する様子が示されており275°の色相角での補正が最大となっている。
色相角による補正範囲を決めるのは(式2)で示される回転関数の色相依存∆θであり、∆θ=0では補正が働かないが増加により補正がきく。(図2)には平均色相角との関係が示されており、
=275°で∆θ=30の最大値となるが、
=230°、320°では∆θ=1.17の値に減少する。
クロマによる補正範囲を決めるのは(式3)で示される回転関数のクロマ依存RCである。前回のスイッチング関数Gが無彩色軸付近での補正を対象としていたが、今回は逆に高クロマが対象になり、無彩色軸付近では補正が効かない様になっている。(図3)によれば、平均クロマ=55以上ではRC=2.00で一定であるが、クロマが減少するにつれ補正が効かなくなる。
以上をまとめると、回転関数の色相依存∆θにより色相角に対する補正範囲が限定され、さらに回転関数のクロマ依存RCにより無彩色軸付近を除いたクロマの補正の結果、回転関数RTにより「青色領域の歪み補正」が行われていることが示された。次回は、色相のT関数による補正について解説を行う。
〈那須野 信行〉



